DuangDuangDuang！铁棍敲黑板！

众所周知，格林公式作为KO与路径无关的第二类曲线积分的杀招，是秀的。但至于为什么适用于路径无关的情况、路径无关的判据为什么是，为什么线积分能够等效成一个二重积分。很多人一脸黑人问号。

煜神学长（考研数学148分天赋选手）和Kaysen学长收到了此类SOS信息，故作本文精讲格林公式的适用条件，从物理本质上吃透该知识点，达到小周天境界。

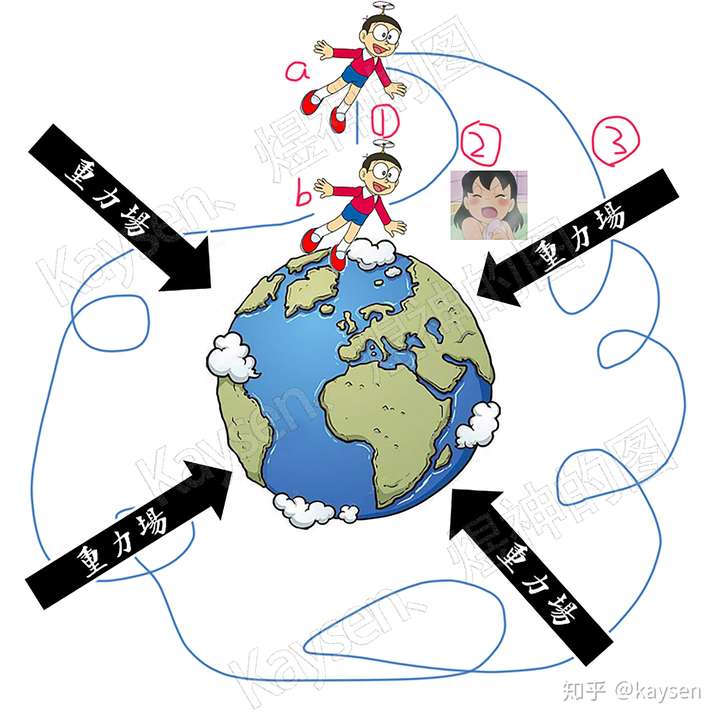
在讲格林公式的路径无关前，先引入一个重力场，假设在屋顶（a点）玩竹蜻蜓的大雄被妈妈喊回去写作业（b点），情况1，竹蜻蜓不好使了，大雄一屁股径直掉到地上，情况2，隔壁的静香在洗澡，害大雄拐了个弯，情况3，风来了，大雄被18级大风吹走了，绕地球转了一圈，不管大雄是哪种路径，只要a,b固定，重力这家伙对大雄做的功都是一毛一样。

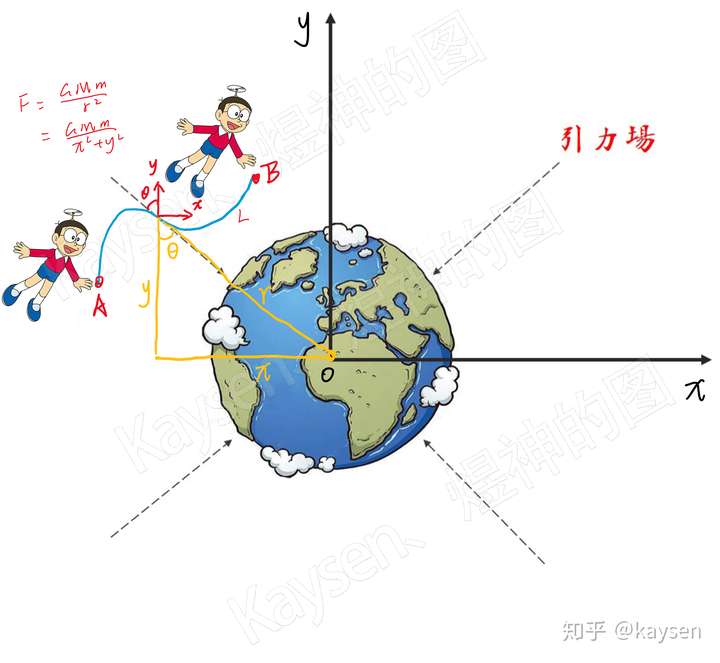
同理，在地球某一个截面的引力场中，引力均从物体指向地心，以地心为原点，做一x/y坐标系，大雄被18级大风从A点吹到B点的过程，问：引力对大雄做功多少？

分析：该模型中，求变力在曲线上做功，即为第二类曲线积分。

任意k点，变化的引力，其中，立即推，。

引力与y轴夹角设为θ，大雄所受引力在x轴和y轴的分量，可表示为，。

引力在AB曲线段对大雄做的功，即为，也即是。

其中，；。（在黄色三角形中，根据勾股定理，可得出，，）

计算一下，，是不是等于，而这是什么？路径无关的判据！是不是很神奇！！！

后面更牛逼，一元的第二类曲线积分，又是怎么能等于一个平面积分（二重积分）的呢？这在弄啥嘞！接着看线积分大变面积分物理魔术！

先来个常识，问你，图中的静香，色彩是连续且密不可分的么？

如果回答是，那就大意了、没有闪！在PS中放大，密不可分的静香是这样式的：

可以看出静香圆润的头型，大大的眼睛，这些曲线，都是由小方块们连在一起，以直代曲，微观为直，宏观为曲，构造而成。而整体上国色天香的静香，也是由许许多多1像素的色块堆积而成。

而以直代曲，用微观的小方块去堆积表达宏观图像，也正是微分学的应用体现。带着这些常识，继续看：

在引力场计算变力做功时，若同一路径来回走一遭，则一来一回的功可相互抵消。

例如一个口字型，可以分解成一个日字型，公共边上的功，相互可消。分成田字形亦然。

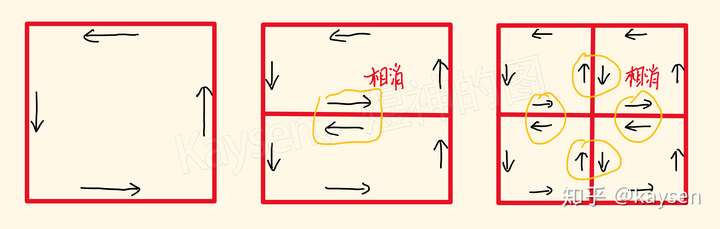
既然引力在曲线上做的功，神tm难算？那么好，我们借助静香图像的讲述，把曲线与曲线围成的图形同时像素化，化作无数像素块堆积而成的平面，那么引力在曲线上沿顺时针方向（或逆时针）做的功，是否可分解成引力沿所有小方块的边顺（逆）所做的功的和？浦东建设股吧###

由于公共边的功正负相消，所以沿小方块们做的功的和，也就演变为小方块堆积图形的轮廓线所做的功，也就是以直代曲下曲线的引力功。

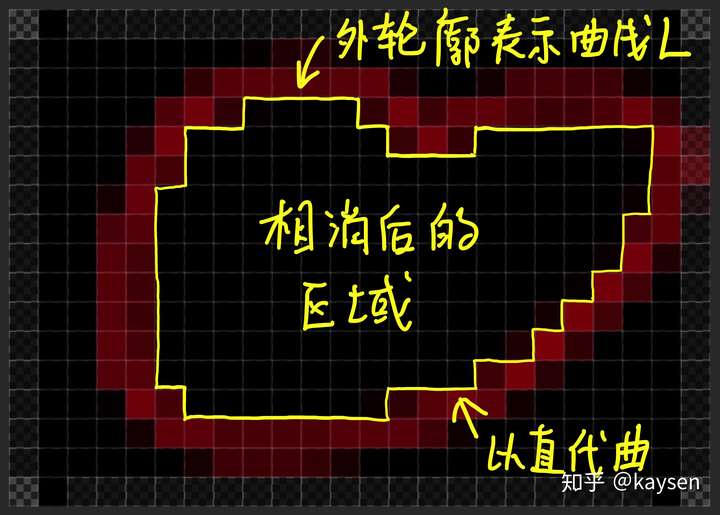
那，这些步骤是怎么在数学上实现的呢？

我们把大雄对静香的爱心，其中一个像素块抽出来，四个点分别赋予坐标值：

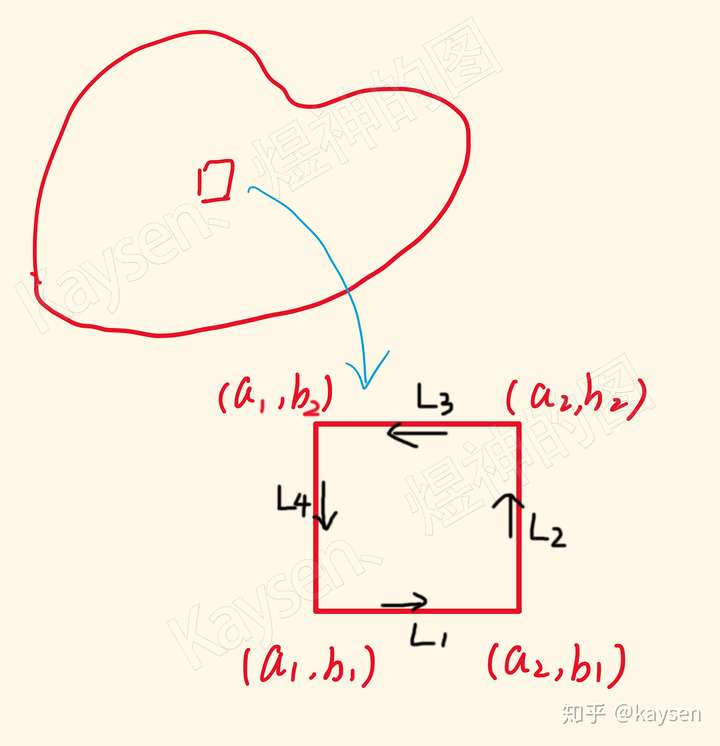
对于单个正方形，引力沿四条边做的功如下：

，

，

求和后，引力沿单个正方形做的总功为（式1）：

插入一个偏导数的极限表达式：

当时，在一阶偏导连续的情况下（格林公式的条件），得到式2式3：

将式2式3回带到式1，有式4：

将式4前部y的上下限互换，整体加负号，有：

此时，引力对单个小正方形做的功已求出，我们想要求爱心曲线上的总功，就把无数个小正方形的功累加即可。在积分上表示为：

于是，格林公式得证！一元的线积分神奇地变成了二重积分！！！

此时，再来首尾呼应下，路径无关为何判据是

变化的引力做功，只与起点和终点相关，那么任意画曲线，曲流拐弯随便拐，只要是从A到B再回到A，引力做功均为0！也就是任意一个面积分，都为0，那么，只有一种可能，被积函数值恒为0。这也就是为什么路径无关，要满足

最后，再来几个反思

煜神问：

1，格林公式处理第二类曲线积分，路径无关怎么理解？再回顾一下本文内容。

2，使用格林公式时曲线为什么要封闭？不封闭为什么要补线？补线为什么要补与坐标轴平行的线？

Kaysen问：

3，在闭区域内存在无定义点时，为什么要挖洞？为什么挖完洞，无定义点就消失了？

4，对问题3进行延伸，既然格林公式能把线积分转化成二重积分，闭曲线内的区域用无数个小方块分割，小方块是可以cover无定义点的，那么只需要计算小方块四条边上的功，不就完美把无定义点的干扰排除了么？那为什么还需要挖洞呢？

希望本文能够启发大家的数学反思，针对数学考点的反思步骤为：

运用公式的本质是？有哪些条件？为什么需要这些条件？条件为什么成立？使用这些条件时有哪些技巧？一步步深挖，将数学彻底建立在反思之上，才能够达到深度理解，解题才能才能得心应手！加油！